傅立叶变换 - 机器学习与信号(一)
什么是信号?维基百科上通俗易懂的解答是:术语「信号」包括音频、视频、语音、图像、通信、地球物理、声纳、雷达、医疗和音乐信号等。本文所说的信号是指时序数据类型的信号,例如声音、心电图等。
Kaggle 比赛中经常会遇到信号处理相关的任务,比如鸟声识别、重力波信号检测 等。
这篇文章稍微系统地梳理一下信号相关任务的一些前置知识和常见的处理方法,因为声音可能是人们接触最多的一种信号,所以本文主要也以鸟声识别(声波)作为例子来讲解。
水平有限,本文不会涉及任何数学细节,只会尝试从宏观的角度去理解
加载音频信号
自然界中的声音是一种连续的机械波,然而计算机只能保存离散的点,那么就需要进行「采样」,即每隔一段时间获取原始信号的数值并记录下来,当这个采样的频率足够高时,保存的声音听上去也就越连续(这里跟视频中的 FPS 是一个道理)。22KHz 是一个常见的音频的采样频率,Hz (赫兹)是频率的单位,表示每秒采样 22000 次。
使用 librosa 中的 get_samplerate 方法可以获取一个音频文件的原始采样率。现在我们尝试获取下面这个音频文件的采样率:
import librosa
librosa.get_samplerate("/assets/fourier-transform/bird.ogg")
32000
原始文件的采样率是 32000 Hz。现在用 librosa.load 加载这个音频文件:
data, rs = librosa.load("/assets/fourier-transform/bird.ogg")
print(f"{data.shape=} {data.__class__.__name__=} {rs=}")
data.shape=(1404025,) data.__class__.__name__=’ndarray’ rs=22050
这里 data 是一个一维的 numpy.array,rs 是采样率,为什么采样率是 22050 呢?因为 librosa.load 默认会对原音频文件进行重采样librosa.resample,将原始的采样数据经过插值等算法变为新的算法,这类似于图像中的 image.resize。
可视化一下这个信号,因为原数据太多,为了方便查看,这里将信号以 10Hz 重采样一次。
import seaborn as sns
resample_rate = 10
data_10hz = librosa.resample(data, rs, resample_rate)
sns.lineplot(data_10hz)

可以看到这是一个似乎没有什么规律的波型信号。
离散傅立叶变换
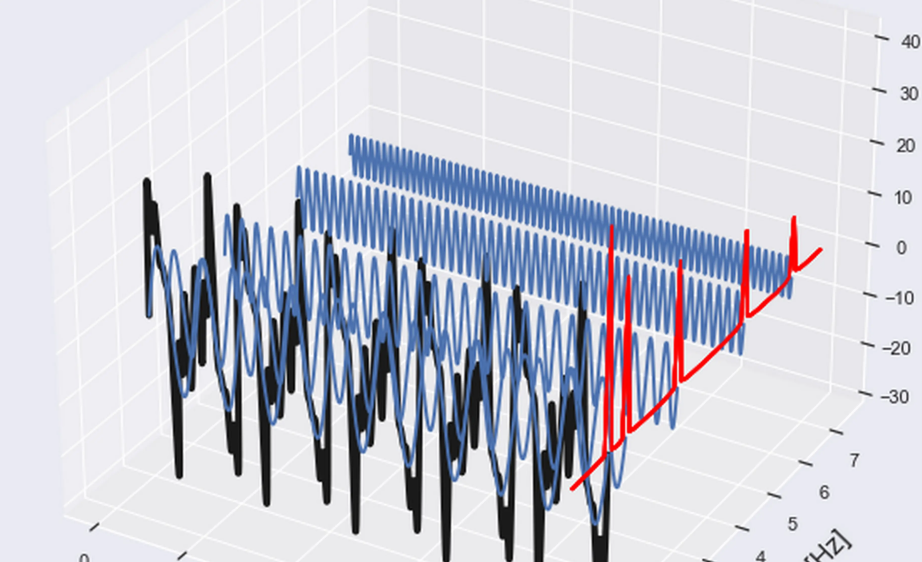
傅立叶变换可以将一上面的音频信号(时域)转换成一堆正弦波之和。而一个正弦波可以通过三个数值来确定:相位(theta)、振幅(A)、频率(k)。也就是说,一个时域信号可以拆成若干个 (theta, A, k) 的元组。这样我们可以以频率为横轴,以振幅或相位做纵轴来画出一个频域上的曲线。这些以频率为横轴的曲线就是频谱图,通过分析某个时域上的波的频谱图,可以获得时域上很难得到的一些结果,因此通过频谱图来分析波是信号处理中很常见的做法。
虽然自然界中大多数信号都是连续的,但计算机中的傅立叶变换都是离散傅立叶变换(Discrete Fourier Transform,简写为 DFT),因为计算机无法存储连续的数据;另外大多数离散傅立叶的实现大多都使用 Fast Fourier Transform 算法以提高性能,简写为 FFT。
下面使用 scipy.fft 模块对上面以 10Hz 重采样的数据(data_10hz)来做傅立叶变换。
from scipy.fft import fft
dataf_10hz = fft(data_10hz)
print(f"{dataf_10hz=} {dataf_10hz.shape=}")
dataf_10hz.shape=(637,) dataf_10hz.shape=(637,)
变换之后的返回值是跟输入的一维信号相同 shape 的向量,这个向量中的每个数值的大小表示某个频率的正弦信号在原信号中的强度,而具体每个数值对应的频率是多少,还需要用下面的代码才能获得:
from scipy.fft import fftfreq
N = len(data_10hz)
frequency = fftfreq(N, 1 / resample_rate) # resample_rate = 10
print(f"{frequency.shape=} {frequency.max()=}")
frequency.shape=(637,) frequency.max()=4.99215070643642
上文说 scipy.fft.fft 返回的向量中,每个元素表示的是某个频率对应的正弦信号强度,也就是说返回的数值对应的频率是不知道的,需要使用 scipy.fft.fftreq 并传入采样率后才能获得 scipy.fft.fft 返回值所对应的频率。其实完整的调用可以这么写:
import numpy as np
resample_rate = 10
yf, frequency = fft(data_10hz), fftfreq(len(data_10hz), 1 / resample_rate)
magnitude, phase = np.abs(yf), np.angle(yf)
print(f"{frequency.shape=} {magnitude.shape=} {phase.shape=}")
frequency.shape=(637,) magnitude.shape=(637,) phase.shape=(637,)
这两个方法同时调用才能获得完整的结果,即不同频率所对应的强度。然后就可以用 frequency 作为横坐标,magnitude 作为纵坐标画出频谱图。
plt.plot(frequency[:N // 2], magnitude[:N // 2])

为什么只画前半部分([:N // 2])?
因为频率的后半部分跟前半部分是镜像的,而中间点频率(N // 2)被称为为奈奎斯特頻率,本文将不再深入。
关于更多傅立叶变换的资料,推荐查看这些的内容:
fourier_video_1 fourier_video_2
短时离散傅立叶变换
比赛中使用得更多的是短时傅立叶变换(Short Time Fourier Transform,简写为 STFT),因为一个时域上的波通常比较长(几十秒到几分钟),直接对这个波做傅立叶变换可能会丢失时间上的信息,因此通常只会对一小段时间做傅立叶变换。
短时傅立叶变换其实就是对一个窗口中的时域信号做傅立叶变换,然后滑动窗口,再做傅立叶变换…因为引入了时间r所以通过短时傅立叶变换,可以获得时间、频率、强度的图像,也称作「时频图」。
现在对上文的原始信号做短时傅立叶变换。
from scipy.signal import stft
f, t, z = stft(
data,
fs=rs, # librosa.load resample 的重采样后的频率,即 22050
window='hann',
nperseg=2048,
noverlap=2048 // 2,
)
print(f"{f.shape=} {t.shape=} {z.shape=}")
f.shape=(1025,) t.shape=(916,) z.shape=(1025, 916)
最后的输出 z 是变换后的数据,也就是时间-频率-强度数据,f,t 分别为频率和时间的值。上面的调用列出了一些重要的参数:
- data 待转换的时域数据。
-
rs 时域数据的采样率。不同于
fft,这里stft在转换的时候就直接传入原始数据采样率,这样就可以直接得到每个强度对应的频率值,而fft还需要配合fftreq才能得到这个值。 -
window 窗函数,默认是
hann,可选用的窗函数参考 scipy.signal.get_window,窗函数类似于 mask,不过这里的 mask 不是只包含 0 1 的矩阵,而是一个更复杂一些的数值。跟一般的 mask 一样,这里的窗函数也是直接与原信号作乘法来获取过滤之后的信号。 -
nperseg 窗口的长度。因为采样率是 22050,因此
nperseg=2048相当于对每 93ms 的时域信号做一次傅立叶变换。 - overlap 控制窗口滑动的步长。
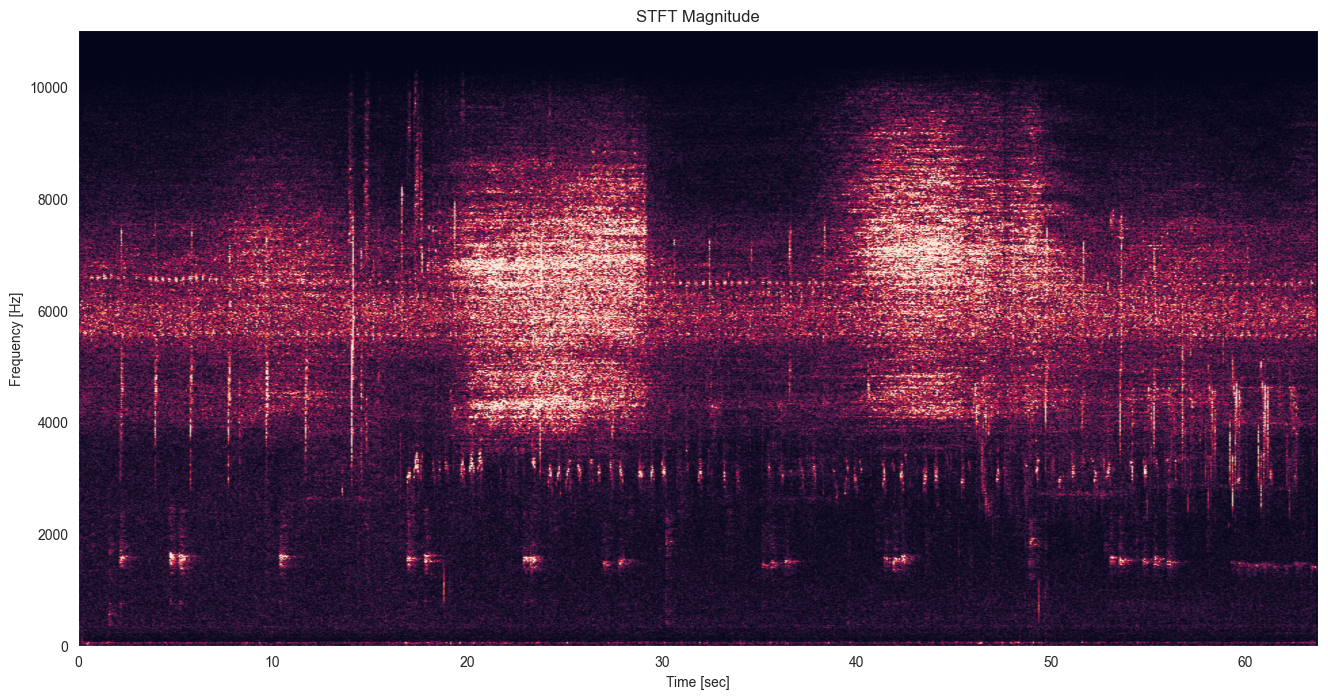
绘制时频图:
magnitude = np.abs(z)
plt.pcolormesh(t, f, magnitude, shading='gouraud', vmin=0, vmax=np.percentile(magnitude, 98))
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()